Съвет 1: Как да намерите основите на трапецовид
Съвет 1: Как да намерите основите на трапецовид
Основите на трапеца могат да бъдат намерени в няколкометоди, в зависимост от зададените параметри. За известна област, височина и страна на равностранен трапец, последователността на изчисленията се свежда до изчисляване на страните на един равнобедрен триъгълник. И също така и за използването на собствеността на равнобедрен трапец.

инструкция
1
Начертайте равностранен трапец. Като се има предвид площта на трапеца - S, височината на трапецовид - h и страната - a. Понижете височината на трапеца към по-голяма основа. По-голямата база ще бъде разделена на сегменти m и n.

2
За да определите дължината на двете основи (x, y), прилагайте свойството на равностранен трапец и формулата за изчисляване на площта на трапеца.
3
Съгласно собствеността на равнобедрен трапец, сегментът nе равна на полу-разликата на основите х и у. Следователно, по-малката база на трапецовия y може да бъде представена като разликата на по-голямата база и сегмента n умножен по две: y = x - 2 * n.

4
Намерете неизвестния по-малък сегмент n. За да направите това, изчислете едната страна на резултантния прав триъгълник. Триъгълникът се формира от височината - h (катет), страни - а (хипотенузата) и сегмента - n (катет). Според питагорейската теорема неизвестната катедрала n2 = a² - h². Заменете известните числови стойности и изчислете квадрата на крака n. Вземете квадратния корен на получената стойност - това е дължината на сегмента n.

5
Заменете тази стойност в първото уравнение за изчисление y. Площта на трапеца се изчислява по формулата S = ((x + y) * h) / 2. Изразете неизвестната променлива: y = 2 * S / h - x.

6
Запишете двете получени уравнения в системата. Замествайки познатите стойности, намерете двете непознати количества в системата с две уравнения. Полученият разтвор на системата х е дължината на по-голямата база и у е по-малката база.

Съвет 2: Как да намерите дължината на основата на трапеца
За да се определи такъв четириъгълник като трапец, най-малко три от страните му трябва да бъдат дефинирани. Следователно, например, можем да разгледаме проблем, в който са дадени дължините на диагоналите трапец, както и един от векторите на страничната страна.

инструкция
1
2
Помислете за триъгълника ABD. Дължината на неговата страна AB е равна на модула на вектора a. Да предположим, че | a | = sqrt ((ax) ^ 2 + (ay) ^ 2) = a, тогава cosφ = ax / sqrt ((ax) ^ 2+ (ay) ^ 2). диагоналното BD има дължина р, и желания AD дължина х. Тогава, с косинусната теорема, P ^ 2 = a ^ 2 + x ^ 2-2axcosf. Или x2 2axcosφ + (a ^ 2-p ^ 2) = 0.
3
Разтвори на квадратното уравнение: Х1 = (2acosf + SQRT (4 (а ^ 2) ((cosf) ^ 2) -4 (а ^ 2-р ^ 2))) / 2 = acosf + SQRT ((а ^ 2) ((cosf) ^ 2) - (а ^ 2-р ^ 2)) == на * брадва | SQRT (((ах) ^ 2 + (AY) ^ 2) + SQRT ((((а) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + p ^ 2) = AD.
4
За да намерите горната основание Sun (дължина в намирането на решения също определени х) се използва модул | а | = а, и втори диагонал BD = р и косинус на ъгъла ABC, което е ясно, равна на (р-р).
5
Триъгълникът ABC, kкойто, както и преди, се прилага косинусовата теорема и възниква следното решение. Като вземем предвид, че cos (n-φ) = -cosφ, въз основа на решението за AD, можем да напишем следната формула, заменяйки p с q: BC = - a * ax | sqrt (((ax) ) + sqrt (((а) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - ^ 2 + q ^ 2).
6
Това уравнение е квадрат и,съответно, има два корена. По този начин, в този случай остава само да се избират онези корени, които имат положителна стойност, тъй като дължината не може да бъде отрицателна.
7
PrimerPust в трапец Страницата ABCD на AB се дава от вектора a (1, sqrt3), p = 4, q = 6. намирам основание трапецРезолюция. Използвайки алгоритмите, получени по-горе, можем да напишем: | a | = a = 2, cosφ = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (sqrt (13) +1) /2.BC=-1/2+sqrt ) = (sqrt (33) -1) / 2.
Съвет 3: Как да намерите височината на трапеца
Трапецът е четириъгълник, yкоито двете страни са успоредни, а другите две не са. Височината на трапеца е сегментът, изчертан перпендикулярно между две успоредни линии. В зависимост от първоначалните данни тя може да бъде изчислена по различни начини.
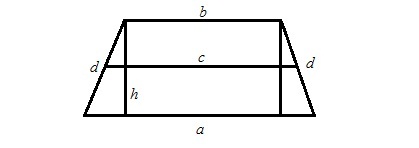
Ще ви трябва
- Познания за страните, основите, средната линия на трапеца, както и, по желание, неговата площ и / или периметър.
инструкция
1
Един начин за изчисляване на площта на трапецае продукт на височина и централна линия. Да приемем, че има трапецовидна осанка. След това височината на равнобедрен трапец с базите a и b, площ S и периметър P се изчислява, както следва: h = 2 x S / (P-2 x d). (виж Фигура 1)
2
Ако само площта на трапеца и нейната база са известни, тогава формулата за изчисляване на височината може да бъде получена от формулата на участъка на трапец S = 1 / 2h x (a + b): h = 2S / (a + b).
3
Да предположим, че има трапец със същите данни катои на фигура 1. Начертаваме 2 височини, получаваме правоъгълник, в който двете по-малки страни са краката на правоъгълни триъгълници. Да обозначим по-малкия за x. Тя се установява чрез разделяне на разликата в дължината между по-големите и по-малките основи. Тогава, по питагорска теорема, квадрата на височината е равна на сумата от квадратите на хипотенузата d и рентгеновия лъч. Извличаме корена от тази сума и получаваме височина h. (Фигура 2)
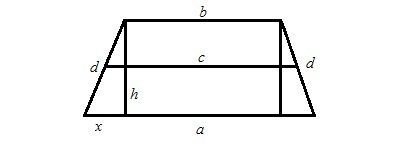
Съвет 4: Как да намерите основите на правоъгълен трапец
Математическа фигура с четири ъгъла се нарича трапец, ако двойката от противоположните й страни е успоредна, а другата двойка не е. Позволяват се паралелни страни бази трапец, другият двустранен. В правоъгълна трапец един от ъглите отстрани е прав.
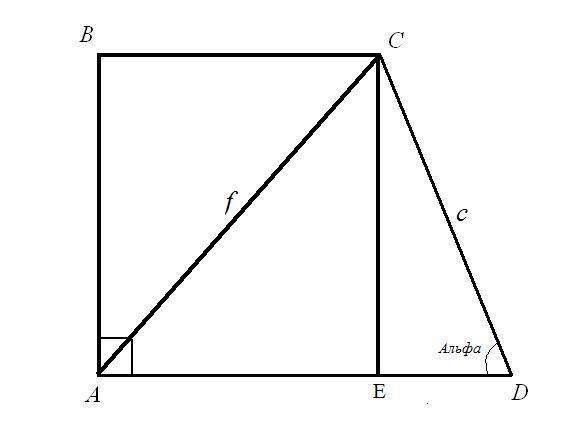
инструкция
1
Задача 1. Намерете основите на BC и AD правоъгълни трапецако дължината на диагонала AC = f е известна; дължинастранична страна CD = c и ъгъла с нея ADC = α. Решение: Помислете за правоъгълния триъгълник CED. Известна хипотенуса c и ъгъла между хипотенузата и крака на EDC. Намерете дължината на страните CE и ED: според формулата на ъгъла CE = CD * sin (ADC); ED = CD * cos (ADC). Така че: CE = c * sinα; ED = c * cosа.
2
Помислете за правилния триъгълник ACE. Хипотенуза AC и CE крак ли, че, да отстрани AE от върховенството на правоъгълен триъгълник: сборът от квадратите на краката е равен на квадрата на хипотенузата. Така че: AE (2) = AC (2) - CE (2) = F (2) - в * sinα. Изчислете квадратния корен на дясната страна на уравнението. Намерихте горната база на правоъгълен трапец.
3
Дължината на базата AD е сумата от дължината на двесегменти AE и ED. AE = квадратен корен (f (2) - c * sinα); ED = c * cosα) Така че: AD = квадратен корен (f (2) - c * sinα) + c * cosα. трапец.
4
Задача 2. Намерете основите на BC и AD правоъгълни трапецако дължината на диагонала BD = f е известна; дължинастранична страна CD = c и ъгъла с нея ADC = α. Решение: Помислете за правоъгълния триъгълник CED. Намерете дължината на страните CE и ED: CE = CD * sin (ADC) = c * sinα; ED = CD * cos (ADC) = c * cosa.
5
Помислете за правоъгълника ABCE. От собствеността на правоъгълника AB = CE = c * sinα. Помислете за правилния триъгълник ABD. Чрез свойството на десен триъгълник квадратът на хипотенузата е равен на сумата от квадратите на краката. Следователно, AD (2) = BD (2) - AB (2) = f (2) - c * sinа. трапец AD = квадратен корен (f (2) - c * sinα).
6
По правилото на правоъгълника BC = AE = AD - ED = корен квадратен (f (2) - c * sinα) - c * cosα. трапец.
Съвет 5: Как да намерите по-малката страна на трапеца
По-малката основа на трапеца е една от нейните успоредни страни, която има минимална дължина. Изчислете тази стойност по няколко начина, като използвате определени данни.
Ще ви трябва
- - калкулатор.
инструкция
1
Ако са известни две дължини - голяма базатрапец и средна линия - използвайте свойството на трапец за изчисляване на най-малката база. Според него средната линия на трапеца е идентична с половината сума от основите. В този случай най-малката база ще бъде равна на разликата в удвоената дължина на средната линия и дължината на голямата основа на тази цифра.
2
Ако знаете такива трапецовидни параметри катоплощ, височина, дължина на голяма база, след това изчислете най-малката база на тази цифра въз основа на формулата на трапецовидната област. В този случай крайният резултат се получава чрез изваждане от разликата на цитираната двойна площ и височината на такъв параметър като дължината на голямата основа на трапеца.
3
Дължината на най-малката страна в правоъгълнаTrapezium се изчислява по друг начин. Този параметър ще бъде равен на произведението от дължината на втората страна и синуса на острия ъгъл, съседен на него. В същите случаи, когато стойността на ъгъла е неизвестна, изравнете най-малката странична страна с височината на трапеца и я изчислете според питагорейската теорема. Най-малката страна в правоъгълния трапец се намира с помощта на косинусовата теорема: c² = a² + b²-2ab * cosα; където a, b, c представляват страните на триъгълника; α е ъгълът между страните a и b.
Съвет 6: Как да намерите по-малката височина на триъгълник
В триъгълника взаимоотношенията между страните и ъглите са твърдо свързани и с вътрешните линии на фигурата - височини, медиани и бисектори. Познаването на тези отношения много опростява решаването на проблемите.

инструкция
1
От трите височини на триъгълника,който се спуска до най-голямата от страните на фигурата. За да видите това, изразявайте трите височини на триъгълника чрез размерите на неговите страни и сравнявайте. Да предположим, че страната a е най-голямата от трите страни a, b, c на произволен триъгълник с остър ъгъл, страната c е най-малката. Означаваме височината h от страната a, hb височината, която е изтеглена към страната b, hc височината към страната c. Височината разделя всеки триъгълник на два правоъгълни триъгълника, в които тази височина винаги ще бъде един от краката.
2
Височината ha, привлечена към най-голямата страна на a,може да се определи от теоремата на Pythagoras: hа² = b² - а₁² или hа² = с² - а₂². Където a1 и a2 са сегментите, към които страната a е разделена на височината ha. Също така, от питагорейската теорема, изразявайте другите две височини на триъгълника през страните му: hb ² = a²-b²² или hb² = c²-b²²; hc2 = a2-c12 или hc2 = b2-c2².
3
От сравнението на формулите, определящи височинитетриъгълник, е очевидно, че съотношението между умаляемото и умалителят дава най-малката разлика по отношение ha² = b² - a₁² и ha² = s²-a₂² като приспадане a₁ и a₂ - големите странични дължини на триъгълник.
4
За да определите по-малката височина на триъгълника, можете да го направитеизвестен също като синуса на ъгъла на триъгълника. Ако условието, повечето от ъглите, а след това този ъгъл се намира срещу най-високата страна, и именно защото се проведе най-ниска височина. За да се избегнат тежки изчисления, по-добре експресират желаната височина чрез тригонометрични функции на другите две ъглите на триъгълника, тъй като съотношението на триъгълника на синуса на ъгъла срещу - стойност за дадена триъгълник е постоянна. Следователно, най-малката височина триъгълник ха = б * SinB или ха = C * Sinc, където В е ъгълът между най-голямата страна на страна и В и С - ъгълът между най-високата страна и страна и триъгълника.







