Съвет 1: Как да намерите района на кръг
Съвет 1: Как да намерите района на кръг
Задачите за изчисляване на площта на едната или другатаГеометричната фигура трябва да бъде решена от студента и студента, геодезиста и архитекта, режещия инструмент. Площта на кръга може да бъде изчислена по различни начини, в зависимост от това какви данни имате.

Основната формула
Около е част от равнината, ограничена откръг. Основният индикатор за кръга и кръга е радиусът. Ако е посочено, площта на окръжността може да бъде изчислена от основната формула S = πR2, където S е областта на окръжността, R е радиусът на окръжността, ограничаващ окръжността, и π е константата равна на 3.14. При условията на проблема може да се даде обиколката. Тя е равна на L = 2πR. В този случай първо трябва да изчислим радиуса, като разделим дадената стойност на L с 2π, т.е. използвайки формулата R = L / 2π.Отстрани на вписаното четиристранно
В кръг, ограничаващ кръг, може да имаВъведено е четиристранно, сумата от противоположните ъгли е 180 °, т.е. квадрат или правоъгълник. В този случай диаметърът на кръга, очертан около квадрата, е едновременно диагонал. Ако размерите на страните на четириъгълника са дадени в условията, не е трудно да се намери този диагонал, използвайки питагорейската теорема. Диагоналът разделя квадрат или правоъгълник на два правоъгълни триъгълника, т.е. това е хипотенузата на всеки един от тези триъгълници. Съответно, може да се намери чрез добавяне на квадратите на страните на четириъгълника, т.е. с формулата d2 = a2 + b2. За да намерите областта на кръга, дори не е нужно да извлечете квадратния корен от получения резултат, защото R = d / 2. За да откриете квадрата на радиуса, достатъчно е квадратът да бъде разделен на 4.На параметрите на триъгълник, вписан в кръг
Методът за решаване на този вариант на проблема зависи от товаТриъгълникът е написан и неговите параметри са дадени. Ако правоъгълен триъгълник, разтвори алгоритъм е същата като за квадрат или правоъгълник като противоположната страна на прав ъгъл, винаги е диаметърът на окръжност кръг. Ако размерът на краката се повдигат всеки от тях в квадрат и да намерят сумата и след това разделяне на резултата от 4 и се умножава по брой П. Ако един триъгълник е равностранен, ще трябва да изпълнява някои допълнителни конструкции, така че в крайна сметка се оказа, правоъгълен триъгълник, чиито параметри, които са известни с теб. Например, окръжност с център О е вписан равностранен триъгълник ABC, от страната на която определя. Изчертайте височините AN, BM и CQ. Помислете, например, за правоъгълен триъгълник AQO. Знаеш ли му AQ хипотенуза, който е равен на половината от страна на първоначалния триъгълник, както и всички ъгли, така че намирането на AQ дължина на отсечката, която също е радиуса на окръжност, чиято площ трябва да намерите, можете да теорема задължително или косинус.Съвет 2: Как да намерите квадрата на квадрат
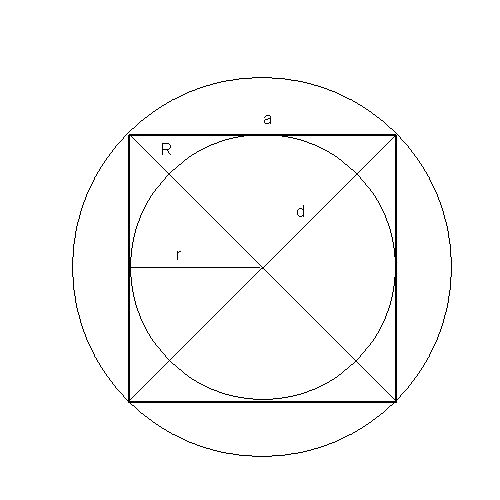
Намерете лицето на фигурата, като квадрат, възможно е дори по пет начина: от страна периметър диагонал радиус на вписан и окръжности.
инструкция
1
Ако дължината на страната на площада е известна, тогава неговатаНапример: a - дължината на страната на квадрата, S - квадрата на квадрата.След това: S = a * a = a² = ъгълът на квадрата е равен на квадрата (втора степен) 11² = 121 мм² Отговор: Квадрат на квадрата със страната 11 мм - 121 мм².
2
Ако е известен периметърът на даден квадрат, тогава неговата площТя е равна на 1/16 от площад (втора мощност) perimetra.Sleduet от факта, че всички (четири) страни на площада са еднакво dlinu.Primer 2.Pust има квадратен периметър с 12 mm.Opredelite ploschad.Reshenie.Oboznachim чрез своята P - периметър на квадрат, S - kvadrata.Togda площ: S = (P / 4) ² = R² / 4² = R² / 16 = 12² / 16 = 144/16 = 9 mm²Otvet: площ на квадрат периметър с 12 mm - 9 mm².
3
Ако радиусът на вписания квадратокръжност, площта му е равна на четири пъти (умножени по 4) на квадрат (втора мощност) radiusa.Sleduet от факта, че радиусът на вписан кръг е равна на половината от дължината страна kvadrata.Primer 3.Pust има квадратна с вписан кръг с радиус от 12 mm.Opredelite площ. Reshenie.Oboznachim чрез: R - радиусът на вписан кръг, S - квадратни, и - страничен дължина kvadrata.Togda: S = ² = (2 * R) = 4 * r² = 4 * 12² = 4 * 144 = 576 mm²Otvet: площ квадрат с радиуса на вписан кръг от 12 mm - 576 mm².
4
Ако радиусът на квадратаокръжност, площта му е равна на два пъти (умножава по 2) на квадрата (втора мощност) radiusa.Sleduet от факта, че радиусът на кръга е равен на половината от диаметъра kvadrata.Primer 4.Pust има квадратен радиус на описаните окръжности 12 mm.Opredelite си ploschad.Reshenie .Oboznachim чрез: R - радиус на окръжност кръга, S - квадратни, и - страничен дължината на квадрат, г - диагонал kvadrataTogda: S = ² = в / 2 = (2R²) / 2 = 2R² = 2 * 12² = 144 = 2 * 288 mm²Otvet: Площ на квадрат с радиуса на окръжност кръг от 12 mm - 288 mm².
5
Ако диагоналът на квадрат е известен, тогава неговата площравна на половината на квадрат (втора мощност) на дължина diagonali.Sleduet теорема Pifagora.Primer 5.Pust има квадрат с диагонал с дължина от 12 mm.Opredelite чрез ploschad.Reshenie.Oboznachim: S - квадратни, г - диагонала на квадрат, и - дължината на страната kvadrata.Togda от Питагоровата теорема: ² + ² = d²S = ² = в / 2 = 12² / 2 = 144/2 = 72 mm²Otvet: Площ на квадрат с диагонал от 12 mm - 72 mm².







