Съвет 1: Как да намерите стойността на израза
Съвет 1: Как да намерите стойността на израза
Числените изрази се състоят от числа, знациаритметични операции и скоби. Ако има такива променливи, то ще се нарече алгебрично. Тригонометричната е израз, в който променливата се съдържа под знаците на тригонометрични функции. Проблемите за определяне на стойностите на числени, тригонометрични, алгебрични изрази често се срещат в учебния курс по математика.

инструкция
1
За да намерите стойността на цифров израз,да определи реда на действията в дадения пример. За удобство го маркирайте с молив над съответните знаци. Извършете всички посочени действия в определена последователност: действия в скоби, експоненциране, умножение, разделяне, добавяне, изваждане. Полученият номер е стойността на цифровия израз.
2
Пример. Намерете стойността на израза (34 ∙ 10 + (489-296) ∙ 8): 4-410. Определете реда на действията. Първото действие се извършва във вътрешни скоби 489-296 = 193. След това умножете 193,8 = 1544 и 34,10 = 340. Следващото действие е 340 + 1544 = 1884. След това разделете 1884: 4 = 461 и след това извадете 461-410 = 60. Намерихте стойността на този израз.
3
За да намерите стойността на тригонометричнитеизразяване при известен ъгъл α, предварително опростяване на израза. За тази цел приложете подходящите тригонометрични формули. Изчислете дадените стойности на тригонометричните функции, заместете ги в примера. Следвайте стъпките.
4
Пример. Намерете стойността на израза 2sin 30º ∙ cos 30º ∙ tg 30º ∙ ctg 30º. Опростете този израз. За тази цел използвайте формулата tg α ∙ ctg α = 1. Получете: 2sin 30º ∙ cos 30º ∙ 1 = 2sin 30º ∙ cos 30º. Известно е, че грехът 30º = 1/2 и cos 30º = √3 / 2. Затова 2sin 30º ∙ cos 30º = 2 ½ √ √3 / 2 = √3 / 2. Намерихте стойността на този израз.
5
Значението на алгебричния израз зависи от товастойността на променливата. За да намерите стойността на алгебричен израз за дадени променливи, опростете израза. Заменете променливите за определени стойности. Извършете необходимите действия. В резултат ще получите число, което ще бъде стойността на алгебричния израз за дадените променливи.
6
Пример. Намерете стойността на израза 7 (a + y) -3 (2a + 3y) при = 21 и y = 10. Опростете този израз, получете: a-2y. Заменете съответните стойности на променливите и изчислете: a-2y = 21-2 ∙ 10 = 1. Това е стойността на израза 7 (a + y) -3 (2a + 3y) за a = 21 и y = 10.
Съвет 2: Как да опростим израза в математиката
Научете се просто да опростите изразите в математикатаНеобходимо е да се решат проблемите и различните уравнения правилно и бързо. Опростяването на израза включва намаляване на броя на действията, което улеснява изчисляването и спестява време.

инструкция
1
Научете се да изчислявате степените с естественииндикатори. Когато умножаване градуса с идентични бази получават мощност на основата на който остава същият и експонентите са добавени б ^ m + б ^ п = б ^ (м + н). Когато разделителни степени с идентични бази получават мощност на основата на който остава същият и експонентите се изваждат и изважда от дивидент индекс експонента делител б ^ м: б ^ п = б ^ (м-н). Когато издигането степен степен превръща мощност на основата на който остава същият, но показателите умножават (б ^ т) ^ п = б ^ (MN) Когато номера експонентни продукта в тази степен се повишава всеки множител. (ABC) ^ m = на ^ m * b ^ m * c ^ m
2
Поставете полиномите в множители, т.е. ги представят под формата на продукт от няколко фактора - полиноми и мономиали. Извършете общия фактор за скобите. Научете основните формули за намалено умножение: разликата между квадратите, квадрата на сумата, квадрата на разликата, сумата от кубовете, разликата от кубовете, куба на сумата и разликата. Например, m ^ 8 + 2 * m ^ 4 * n ^ 4 + n ^ 8 = (m ^ 4) ^ 2 * m ^ 4 * n ^ 4 + (n ^ 4) ^ 2. Тези формули са основни в опростяването на изразите. Използвайте метода за извличане на пълен квадрат в триномия на формата ax ^ 2 + bx + c.
3
Намалете фракциите колкото е възможно по-често. Например, (2 * a ^ 2 * b) / (a ^ 2 * b * c) = 2 / (a * c). Но не забравяйте, че можете да отрежете само множители. Ако числителят и знаменателят на алгебрична фракция се умножат по същия номер, различен от нула, тогава стойността на фракцията не се променя. Можете да трансформирате рационални изрази по два начина: по верига и по действие. За предпочитане вторият метод, защото По-лесно е да проверите резултатите от междинните действия.
4
Често в изразите е необходимо да се извлекат корените. Корените на равна степен се извличат само от негативни изрази или числа. Корените на странна степен се извличат от всички изрази.
Съвет 3: Как да намерите стойността на тригонометричните функции
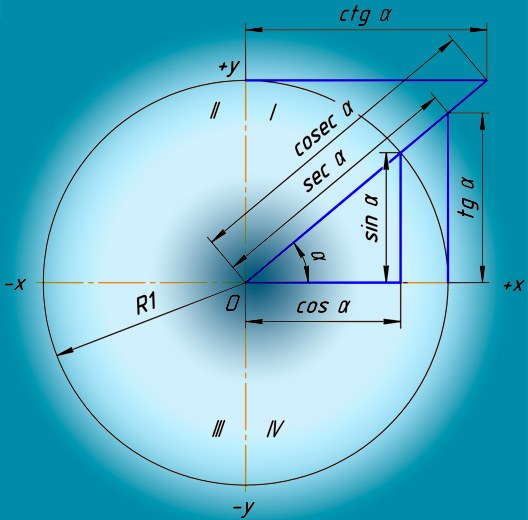
Първоначално тригонометричните функции се появяват катоинструменти за абстрактно математическо изчисляване на зависимостите на острите ъгли в правоъгълен триъгълник по дължината на неговите страни. Сега те са широко използвани в научните и техническите сфери на човешката дейност. За практически изчисления на тригонометричните функции от дадените аргументи можете да използвате различни инструменти - някои от най-достъпните са описани по-долу.
инструкция
1
Използвайте, например,по подразбиране, заедно с операционната система, програма за калкулатор. Той се отваря, като изберете елемента "Калкулатор" в папката "Сервиз" от подраздел "Стандарт", поставен в секцията "Всички програми". Този раздел може да бъде намерен, като кликнете върху бутона "Старт" в главното меню на операционната система. Ако използвате версията на Windows 7, можете просто да въведете думата "Калкулатор" в полето "Намиране на програми и файлове" в главното меню и след това да кликнете върху съответната връзка в резултатите от търсенето.
2
Въведете стойността на ъгъла, за който искатеизчислете тригонометричната функция и след това кликнете върху съответния бутон - sin, cos или tan. Ако се интересувате от обратни тригонометрични функции (arcsine, arc cosine или arctangent), първо щракнете върху бутона с надпис Inv - той променя функциите, присвоени на контролните бутони на калкулатора, към противоположните.
3
В по-ранните версии на операционната система (например Windows XP)За да получите достъп до тригонометричните функции, отворете секцията "Преглед" в менюто на калкулатора и изберете реда "Инженеринг". Освен това, вместо интерфейса на по-старите версии на програмата, вместо бутона "Inv" има квадратче със същия надпис.
4
Можете да направите без калкулатор, ако иматеима достъп до интернет. Има много услуги в мрежата, които предлагат различно организирани калкулатори на тригонометрични функции. Един от най-удобните опции е вграден в търсачката Nigma. Отидете на основната си страница, просто въведете стойността, която ви интересува, в полето за търсене - например "arctangent 30 degrees". След като кликнете върху бутона "Търсене!", Търсещата машина изчислява и показва резултата от изчислението - 0,482347907101025.
Съвет 4: Намиране на значението на изразите
Някои родители, които помагат на по-малките си децаучениците в домашните по математика, попадат в сляпа алея, забравяйки правилата за намиране на смисъла на израза. Много въпроси възникват по правило в процеса на решаване на задачи от програмата на 4-ти клас. Това се дължи на увеличаването на броя на писмените изчисления, появата на многоцелеви номера, както и на действията с тях. Независимо от това, тези правила са доста прости и са много лесни за запомняне.

Ще ви трябва
- - учебник;
- - Проект;
- - дръжката.
инструкция
1
Пренапишете математическия израз от учебника в чернова. Инструктирайте детето да направи всички изчисления на първо място в черновата, за да избегнете замърсяване в работната книга.
2
Изчислете броя на необходимите действия имислете в какъв ред да бъдат изпълнени. Ако този въпрос затруднява за вас, имайте предвид, че преди другите, действията в скоби се извършват, а след това - разделяне и умножение; Добавянето и изваждането се извършват последно. За да улесни детето да запомни алгоритъма за действията, които трябва да се изпълнят, в израза над всеки знак на оператор (+, -, *, :) с тънък молив, поставете числата, съответстващи на реда на действията.
3
Преминете към първото действие,придържайки се към установения ред. Обмислете в съзнанието си дали действията са лесни за изпълнение. Ако се изискват писмени изчисления (в колона), запишете ги под израза, посочвайки поредния номер на действието.
4
Очевидно наблюдавайте последователността отдействия, оценявайте какво трябва да се изважда, какво да се разделя и т.н. Много често отговорът в израза се оказва неточен поради грешките, направени на този етап.
5
Обърнете внимание, че детето не използва калкулатор в изчислителния процес, тъй като в този случай целият смисъл на изучаването на математиката, който се състои в развитието на логиката и мисленето, се губи.
6
Не решавайте задачите на детето - нека го направинаправете го сами, просто трябва да ръководите действията му в правилната посока. Извикайте в паметта му, помолете го да помни как учителят обясни материала по време на урока.
7
Извършване на всички действия и намиране значение изразът, който е отговорът в последното действие, го напишете в състоянието на израза след знака за равенство.
8
Ако в края на урока се дадат отговори на задачите, сравнете резултата с правилния номер. В случай на несъответствие с данните, преминете към преизчисляването.
Съвет 5: Какви са цифрови изрази
Изразите са основата на математиката. Концепцията е достатъчно широка. Повечето неща, които трябва да се разгледат в математиката - и примери, уравнения и дори фракции - са изрази.

Отличителна черта на израза еналичие на математически действия. Показва се чрез определени знаци (умножение, разделяне, изваждане или прибавяне). Последователността на математическите действия се коригира със скоби, ако е необходимо. Извършването на математически действия означава намиране на смисъла на израз.







